1. If 3x + 5 = 14, x² =
Answer:
2. A rectangular tank is 2 meters by 4 meters by 5 meters. If a jug can hold 4 cubic meters of water, how many of these jugs can empty into the tank?
Answer:
3. In △XYZ below, x =
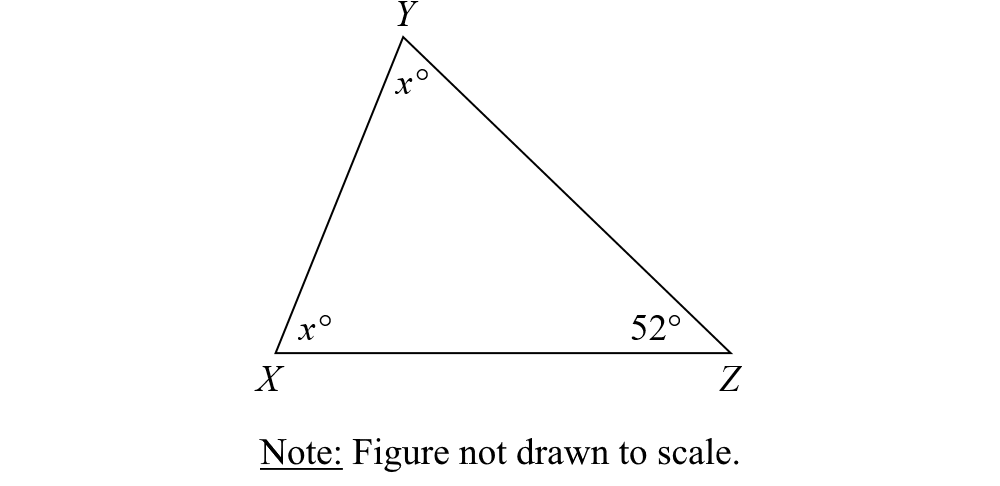
Answer:
4. If (n - 1)(1/(n + k)) = 1, then k =
Answer:
5. If the sum of two integers is 22 and the product of the same two integers is 105, then the positive difference between the two integers is
Answer:
6. When did the population of City A experience the greatest absolute change?
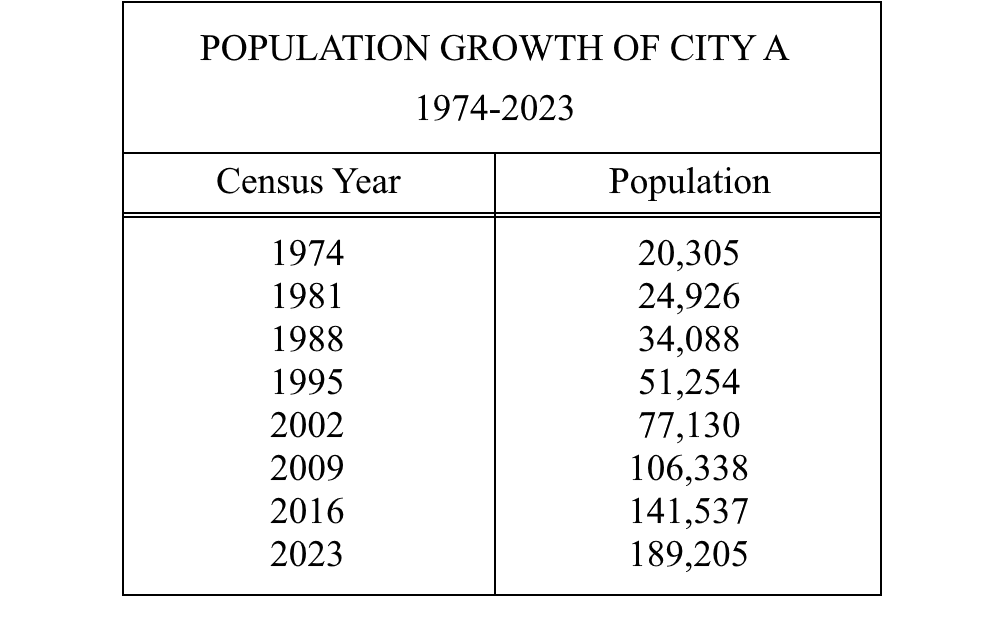
Answer:
7. A pet shop only sells fish, parrots, and turtles. 1/2 of the pets are fish, 2/5 are parrots, and the rest are turtles. What is the ratio of the number of turtles to the number of fish?
Answer:
8. In the figure below, a circle with radius r rests in the second quadrant and just touches the x- and y-axes. What are the coordinates of T, the uppermost point of the circle?
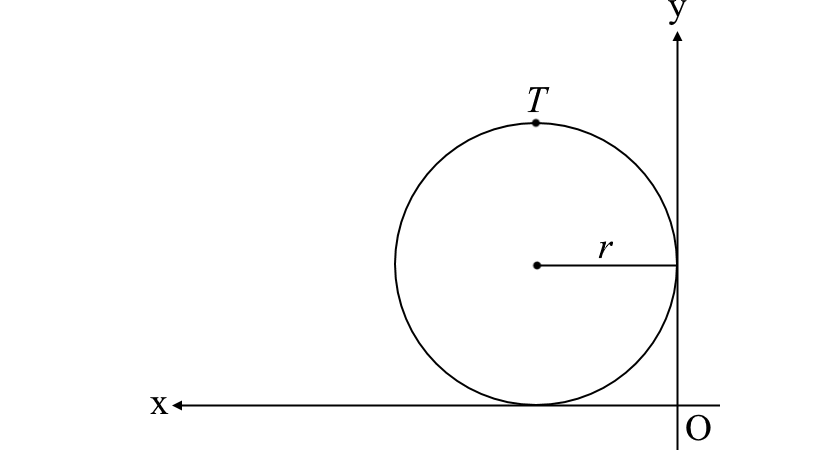
Answer:
9. If p is 60 percent of q and q is 75 percent of r, then r/p =
Answer:
10. In the figure below, x + y =
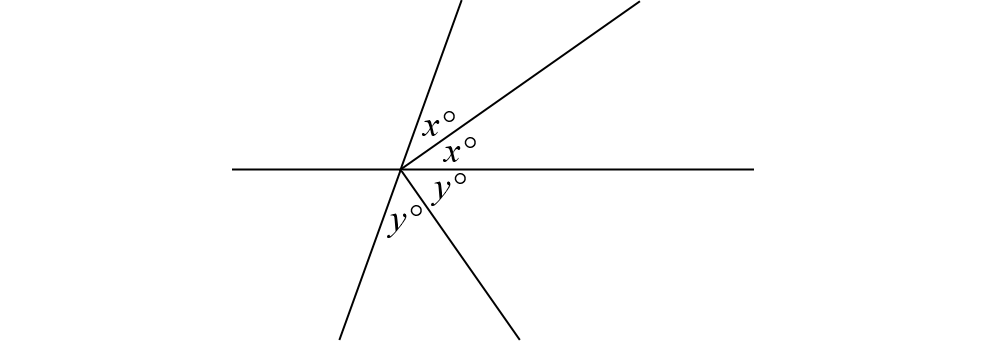
Answer:
11. If √(1,000 + x) equals an integer which of the following could be the value of x?
Answer:
12. Tony bought two dozens of eggs and 15 slices of cheese for $9.00. If a slice of cheese costs $0.20, how much does one egg cost? Note: There are 12 in one dozen.
Answer:
13. In the figure below, if Q is the midpoint of PR, then QS =
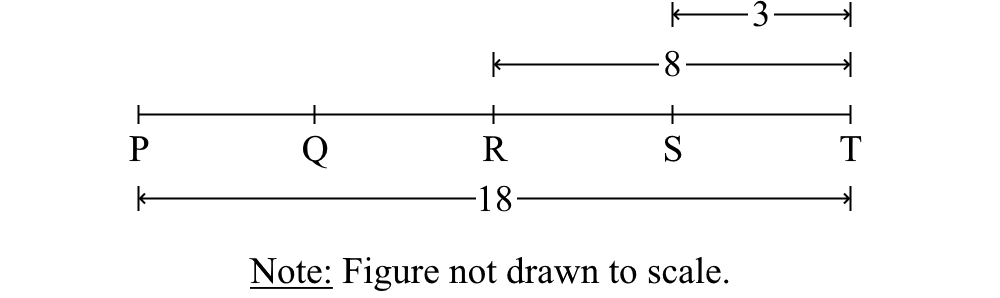
Answer:
14. The set P consists of all numbers that are multiples of 3 but not factors of 144. How many numbers in P are in between 25 and 50?
Answer:
15. If the first day of a month with 31 days is Saturday, what day is the last day of the month?
Answer:
16. If the figure below is cut into two pieces by making a straight cut, what would be the greatest total number of edges possible on the two pieces?
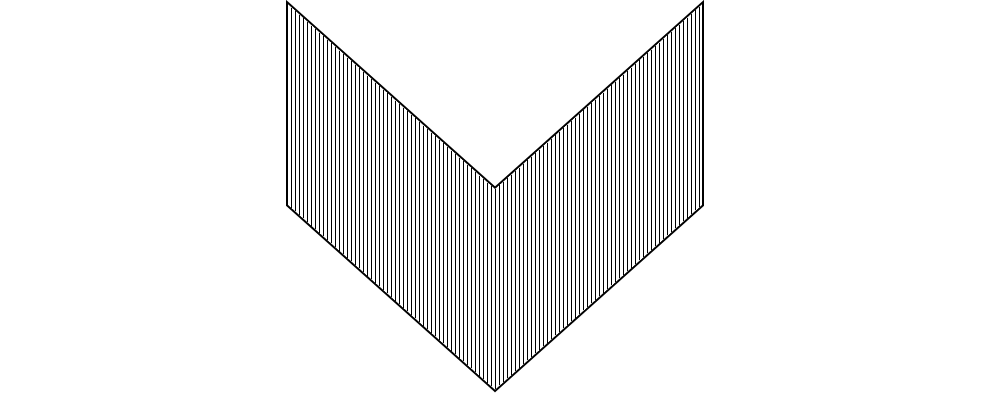
Answer:
17. If m and n are integers such that m/n = 1/4, which of the following could be the value of m + n?
Answer:
18. Which of the following must be even?
I. The sum of two prime numbers greater than 2
II. The product of two prime numbers greater than 2
III. The sum of I and II
Answer:
19. In the figure below, x =
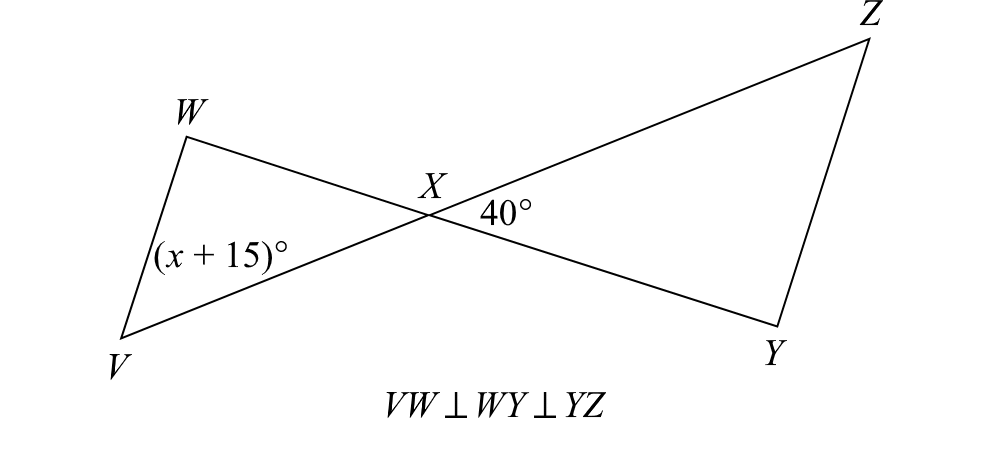
Answer:
20. There are three horses in a horse race. Horse A finishes a lap in 3 minutes. Horse B finishes a lap in 4 minutes. Horse C finishes a lap in 5 minutes. All three horses start racing at the same point on the track. By the time all three horses align at the same point again, how many laps will horse A have completed?
Answer:
21. A suit and tie cost $550 altogether. The suit costs $500 more than the tie. If you pay $100 for just the tie, how much change should you receive?
Answer:
22. Starting from the second row, each number in a row is the sum of 7 and the corresponding number in the row above, with only the units digit retained. If a sixth row is added in this fashion, which row would have the smallest sum of its numbers?

Answer:
23. (4 ⋅ 5 ⋅ 9 ⋅ 14)/(6 ⋅ 7 ⋅ 10 ⋅ 15) =
Answer:
24. The time displayed on an analog clock is 6:00. How many times will the minute hand overlap with the hour hand in the next 12 hours?
Answer:
25. If the area of square ABCD is 48, what is the length of the circular arc AC?
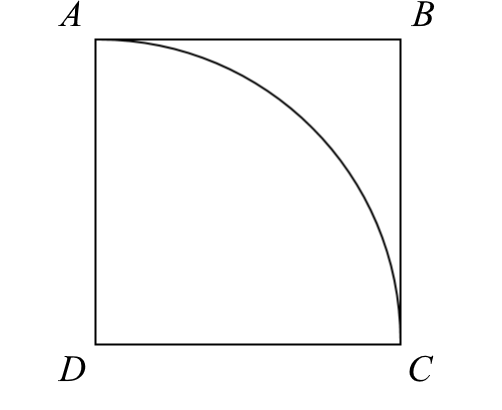
Answer:
26. If 1/(2x) = 4 and 16x = y, then (2xy³)⁴ =
Answer:
27. A professional typist can type 200 words in t minutes. If a novel has 500 words in each page, how many pages in the novel can the typist type in x hours?
Answer:
28. The coordinates of points P, Q, and R are shown in the figure above. Where should point S be placed to create a quadrilateral PQRS of area 15?
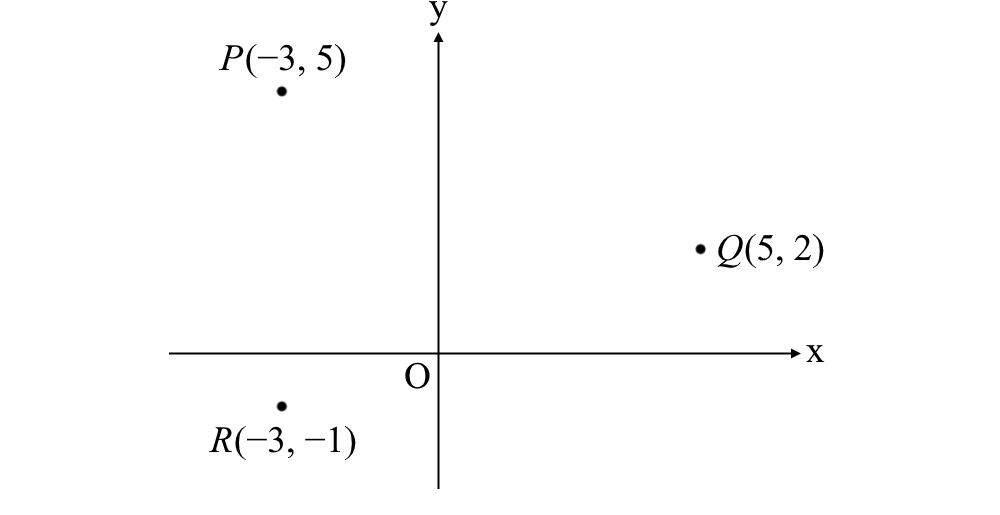
Answer:
29. For any positive integer k, define [k] by the equation [k] = k^2 - k; for example [5] = 20. Which of the following statements must be true?
I. [2][3] = [4]
II. 6 is a multiple of [6]
III. [k] is a factor of k - 1
Answer:
30. If a right triangle has a hypotenuse of length 15 and all of its sides have integer lengths, what is the sum of the lengths of the two smaller sides of this triangle?
Answer:
31. In the die below the number of dots on each pair of opposite faces sum to 7. If the die can be rotated into any orientation where three faces are shown, what is the greatest difference in the sum of the number of dots on the three visible faces?

Answer:
32. Leo produces n units in 4 hours, while Same produces n units in 6 hours. If Leo and Sam work at the same time, how long would it take them to produce n units together?
Answer:
33. How many times will the digit 1 be written when listing the integers from 1 to 100?
Answer:
34. The arithmetic mean in a set of six distinct integers is 15. If the largest integer in the set is 20, what is the maximum possible value of the smallest integer?
Answer:
35. The area of the circle below with center O is 12π. If 90 < x < 180, what are all possible values for side length PQ of triangle OPQ?
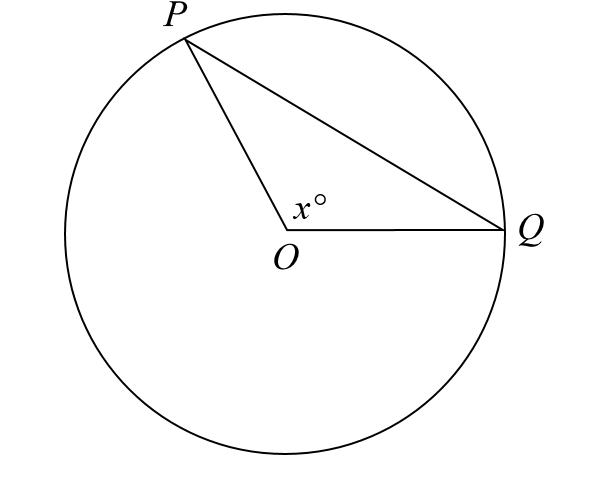
Answer:
36. In a 364-meter building, each floor is a 4 meters high. On odd floors there are an even number of windows. On even floors, there are an odd number of windows. Which of the following could be the total number of windows in this building?
Answer:
37. If a triangle △ABC has side lengths such that AB < BC < CA, which of the following must be true?
Answer:
38. If the figure below, two circles of the same size lie on the same horizontal plane and intersect at a point. The line segment PS connects the uppermost point of the left circle to the lowermost point of the right circle. If PS = 8, what is the sum of the shaded areas?
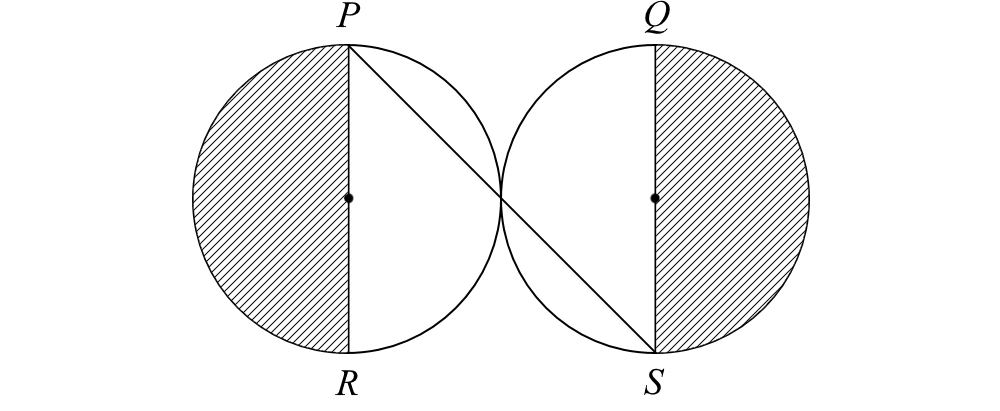
Answer:
39. A set of consecutive integers starts at -27. If the sum of all integers in this set is 252, how many integers are there in the set?
Answer:
40. If xy > 0 and xyz < 0, which of the following statements must be true?
I. x + y > 0
II. xy > yz
III. xz < xyz
Answer:
41.
A. -0.90
B. -0.909
Answer:
42.
a = 2b
A. a²
B. 2ab
Answer:
43.
A. The volume of a cube with side length π
B. The area of a circle with radius π
Answer:
44.

A. x B. 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1
Answer:
45.
4k - 5 = -13
A. k
B. -k²
Answer:
46.
The ratio of 2 to 3 equals the ratio of sqrt(x) to 9.
A. x
B. 2⁶
Answer:
47.

A. The cost of a 1-hour lesson with Teacher A B. The cost of a 1-hour lesson with Teacher B
Answer:
48.
x < -1
y > 1
A. xy
B. x/y
Answer:
49.
-9 < m < n < -3
A. m - n
B. -6
Answer:
50.
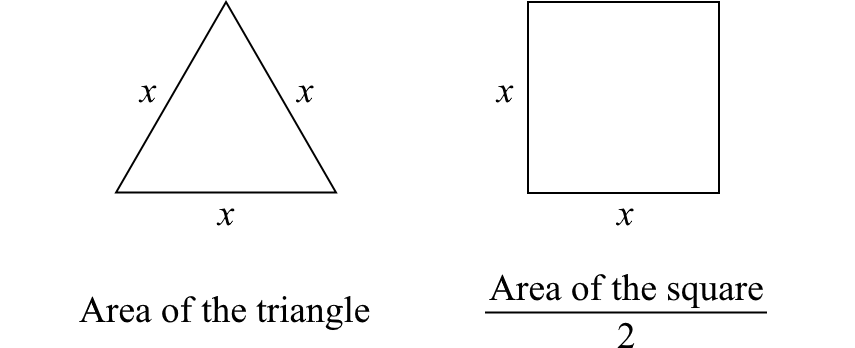
A. area of the triangle B. area of the square / 2
Answer:
51.
20% of p is 80% of q.
p and q are nonzero values.
A. p²
B. 15q²
Answer:
52.
A set of 18 cookies each worth $0.34 costs c dollars and d cents.
A. c/(100d)
B. 1/50
Answer:
53.
A. The total number of pentagons that can be named in the figure above B. 8
Answer:
54.
4r > 3s
r < s
r and s are positive integers
A. rs
B. 20
Answer:
55. The length of rectangle B is 10 percent less than the length of rectangle A, and the width of rectangle B is 10 percent greater than the width of rectangle A.
A. Area of rectangle A
B. Area of rectangle B
Answer:
56.
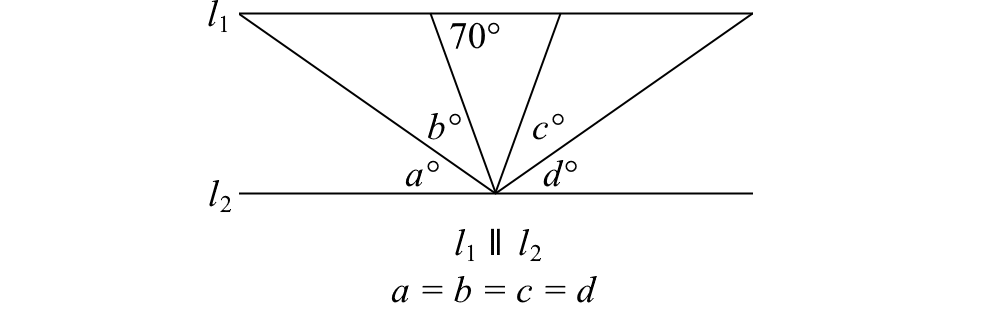
A. b + 2c + 3d B. The product of the first four prime numbers
Answer:
57. The arithmetic mean of k and k² + 1 is greater than 15.
A. k
B. 4
Answer:
58. The product of two integers is 12.
A. The number of different values for one of the integers possible
B. 12
Answer:
59.
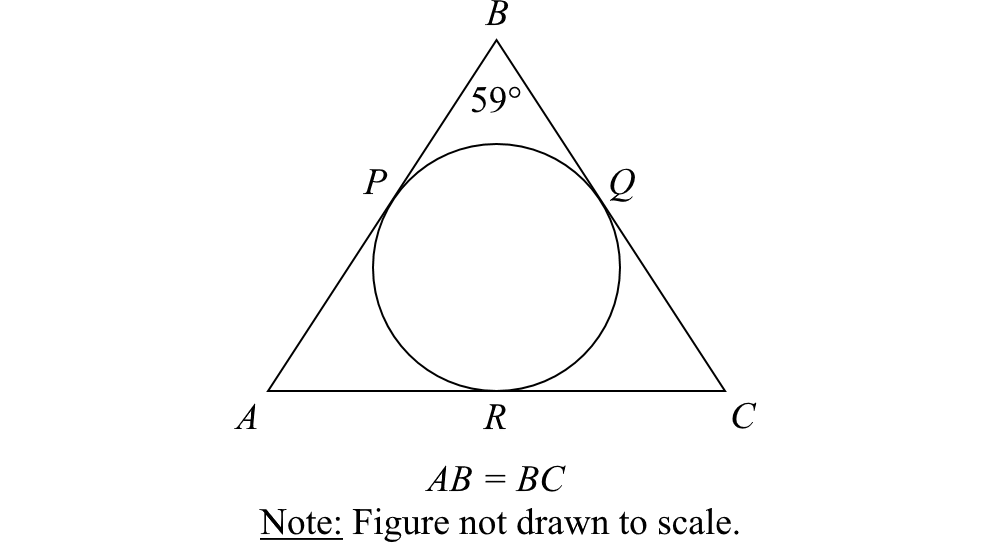
A. Arc length PQ B. Arc length QR
Answer:
60.
x + 5 is 25% of y²
x and y are integers between 1 and 9 inclusive.
A. x
B. y
Answer:
61.
A. (1/5)¹⁰
B. (1/10)⁷
Answer:
62.
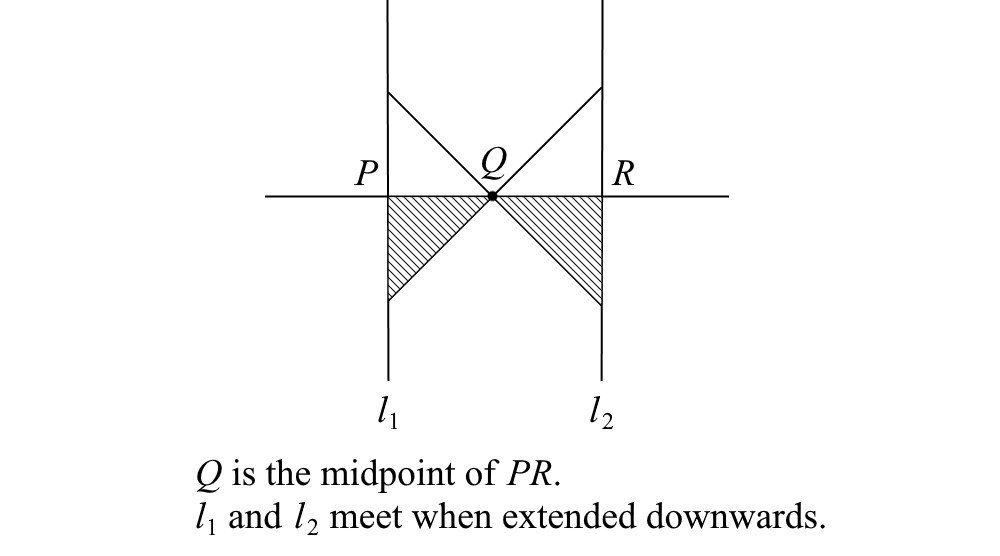
A. The sum of the areas of the shaded triangles B. The sum of the areas of the unshaded triangles
Answer:
63. Set W consists of the numbers 3, 5, 6, 8, and x, where x is a positive integer. y is the arithmetic mean of Set W and is less than the median of Set W.
A. x
B. y
Answer:
64. In a class of 150 students, 140 students are enrolled in math, 110 students are enrolled in science, and 75 students are enrolled in art.
A. The smallest fraction of students enrolled in all three classe
B. (4²)%
Answer:
65.
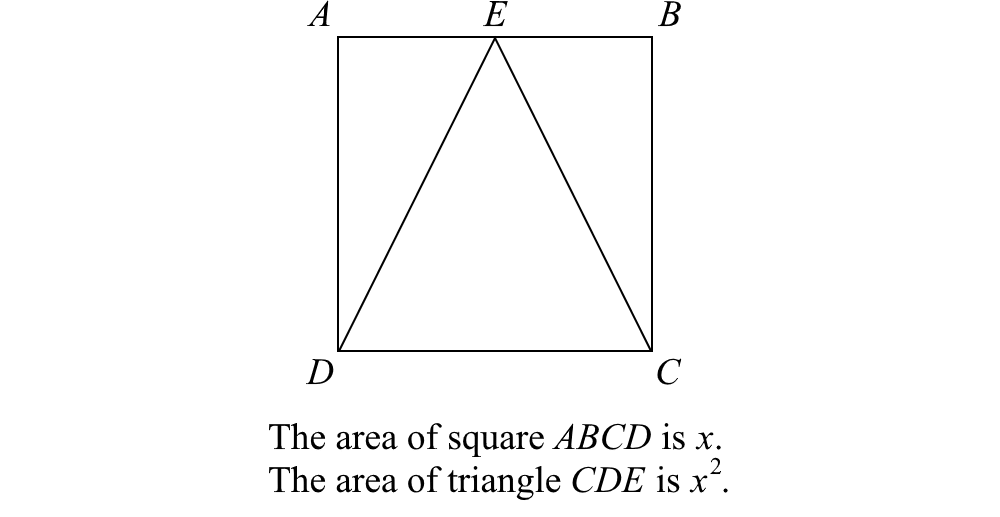
The area of square ABCD is x. The area of triangle CDE is x^2.
A. AB B. Area of triangle CDE / Area of square ABCD
Answer:
66. A pyramid is built using identically sized blocks. The first level consists of one block. Every succeeding level is formed by placing blocks around the previous level in a manner that increases the grid dimensions by two in each direction. If the pyramid has seven levels, what is the sum of the number of blocks on the odd-numbered levels?
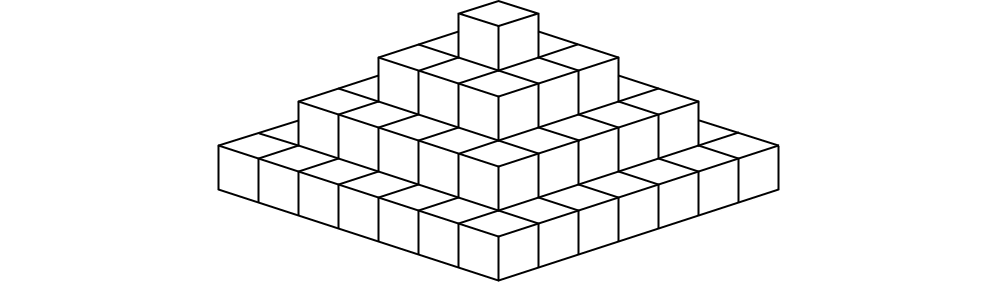
Answer:
67. Two isosceles right triangles have areas X and Y, respectively. If x and y are the respective hypotenuses of the two triangles, then, in terms of their area, x + y =
Answer:
68. A bus located at point P needs to travel to point Q. The bus can travel along any of the given lines but cannot arrive at the same point twice (including P). How many different paths can the bus take?
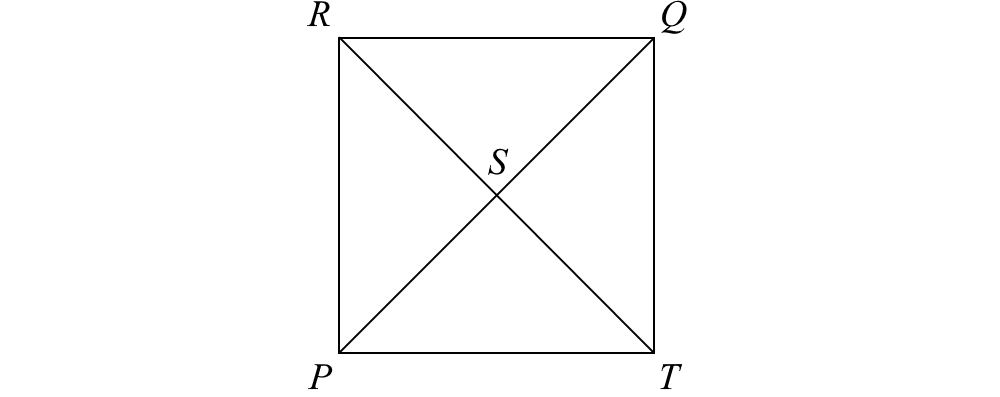
Answer:
69. If x represents the product of all the integers between 1 and 30 inclusive, what is the smallest positive integer that is not a factor of x and is not a prime number?
Answer:
70. A cube has a side length of 1. The vertex-to-vertex distance is the straight-line distance between any two vertices on the cube. If x and y represent the greatest and least possible vertex-to-vertex distances on this cube respectively, x - y =
Answer:
71.
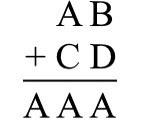
In the addition problem above, A, B, C, and D represent distinct digits from 1 to 9. How many different values of D are possible?
Answer:
72. A rectangular garden measures 40 feet by 60 feet. If a gardener wants to double its area by adding an equal width of land around its perimeter, how wide should the strip of land be?
Answer:
73. In an orchestra of 100 musicians, 25% are wind instrument players and more than 60% are string instrument players. If x musicians are both wind and string instrument players, and 2x of them are neither, which of the following could be the number of people who are both wind and string instrument players?
Answer:
74. A circular sector with a central angle of 120° is cut and folded into a cone. What will be the ratio of the base radius to the height of the cone?
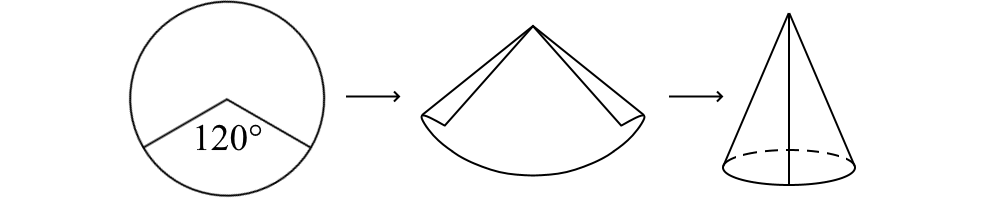
Answer:
75. A square is inscribed inside a circle with radius x. Inside this square, another circle is inscribed. Inside this smaller circle, another square is inscribed. If y is the perimeter of this smaller square, which of the following could be equal to 1/2?
I. 2x/y
II. √(x/y)
III. (x + y)/(x² + y²)
Answer: